Hack-A-Sat 2021: Fiddlin' John Carson
Category: Satellite Operations
Points: 22
Challenge
Where do you come from?
Connect to the challenge on:
derived-lamp.satellitesabove.me:5013
Observations
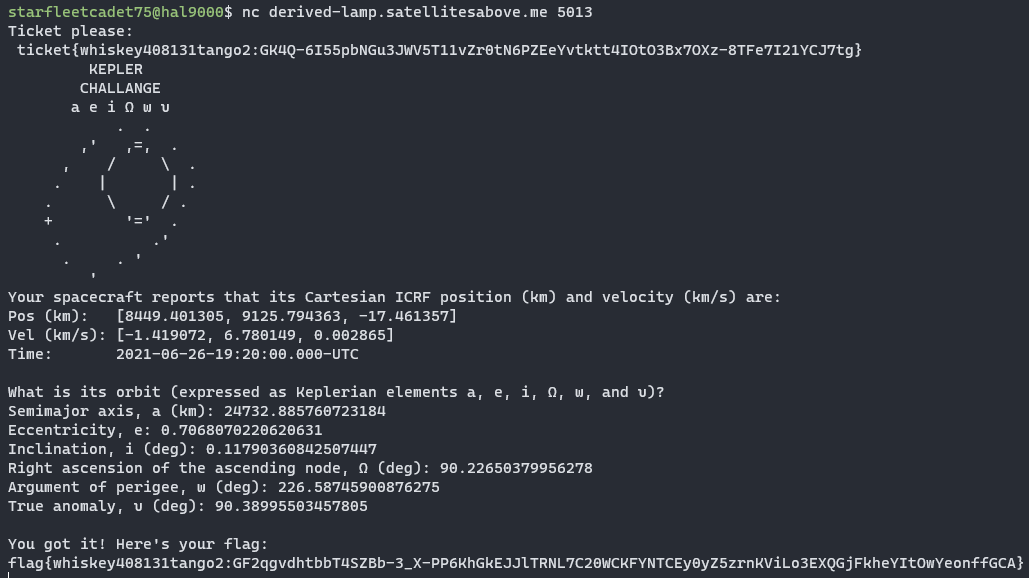
Connecting to the challenge server presents us with a nice ASCII art of a planet with an orbiting spacecraft.
KEPLER
CHALLANGE
a e i Ω ω υ
. .
,' ,=, .
, / \ .
. | | .
. \ / .
+ '=' .
. .'
. . '
'
Your spacecraft reports that its Cartesian ICRF position (km) and velocity (km/s) are:
Pos (km): [8449.401305, 9125.794363, -17.461357]
Vel (km/s): [-1.419072, 6.780149, 0.002865]
Time: 2021-06-26-19:20:00.000-UTC
What is its orbit (expressed as Keplerian elements a, e, i, Ω, ω, and υ)?
Semimajor axis, a (km):
The challenge provides us with a set of orbital state vectors (position, velocity, and epoch) that describe the trajectory of the orbiting spacecraft. We are asked to determine the Keplerian elements for this orbit, which are a set of parameters that can uniquely describe the orbit of an object in space and are based on Johannes Kepler’s laws of planetary motion.

The elements are as follows:
- Semimajor axis, a (km): the distance between the centers of the bodies
- Eccentricity, e: the shape of the ellipse
- Inclination, i (deg): the vertical tilt of the ellipse
- Longitude of the ascending node, Ω (deg): horizontally orients the ascending node of the ellipse
- Argument of perigee, ω (deg): defines the orientation of the ellipse in the orbital plane
- True anomaly, υ (deg): defines the position of the orbiting body along the ellipse at a specific time
These elements are commonly encoded as TLEs, which are used for sharing orbital information for satellites.
Solution
poliastro supports creating Orbit objects from state vectors.
We can then easily access each Kepler orbital element and convert them to the proper units.
from astropy import units as u
from astropy.time import Time
from poliastro.bodies import Earth
from poliastro.twobody import Orbit
r = [8449.401305, 9125.794363, -17.461357] * u.km
v = [-1.419072, 6.780149, 0.002865] * u.km / u.s
t = Time("2021-06-26T19:20:00.000")
orb = Orbit.from_vectors(Earth, r, v, epoch=t)
print(f"Semimajor axis: {orb.a}")
print(f"Eccentricity: {orb.ecc}")
print(f"Inclination: {orb.inc.to(u.deg)}")
print(f"Longitude of the ascending node: {orb.raan.to(u.deg)}")
print(f"Argument of perigee: {orb.argp.to(u.deg)}")
print(f"True anomaly: {orb.nu.to(u.deg)}")
Entering each of the values prints our flag: